MECHANICS OF SOFT DIELECTRIC MEMBRANES
|
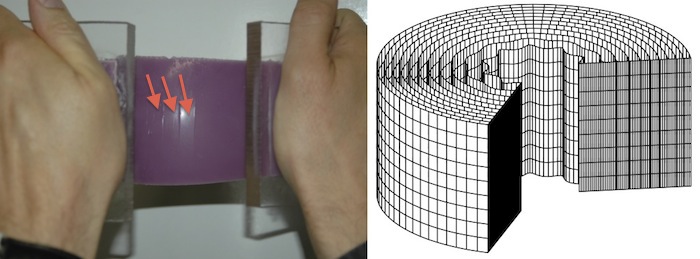
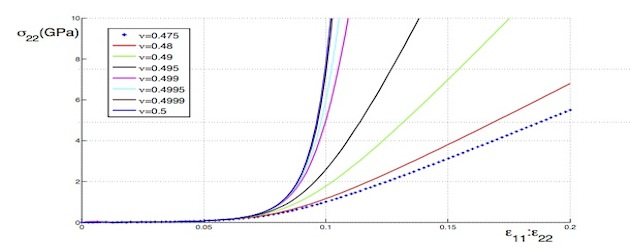
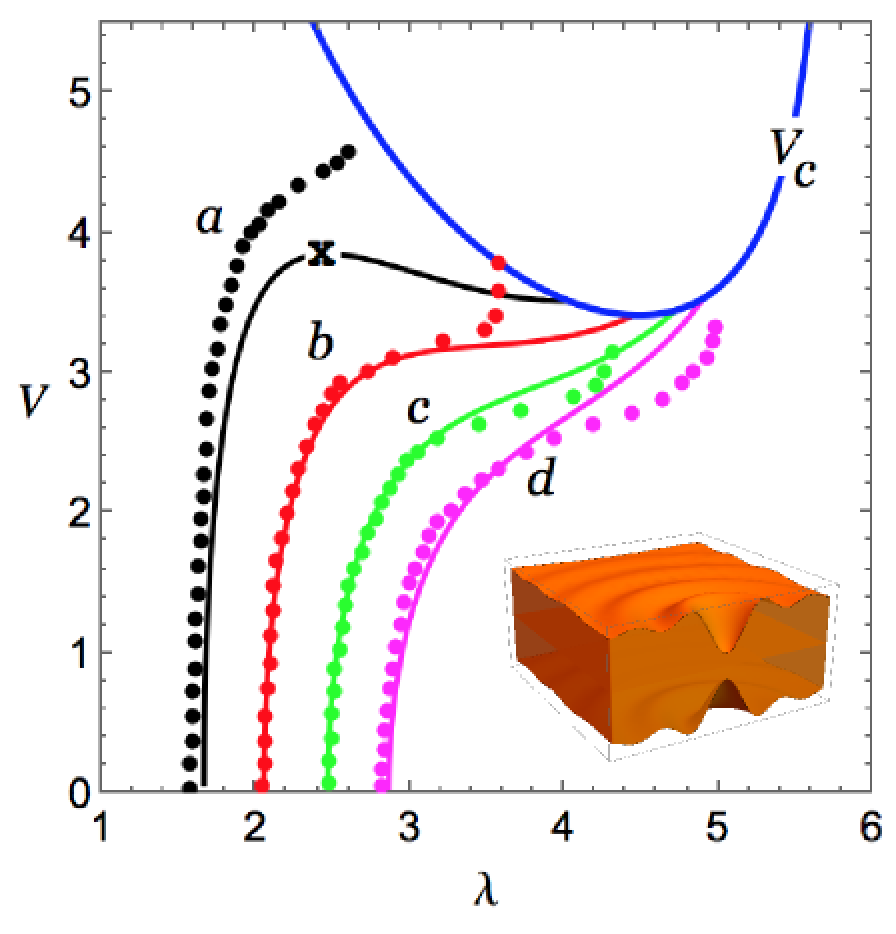
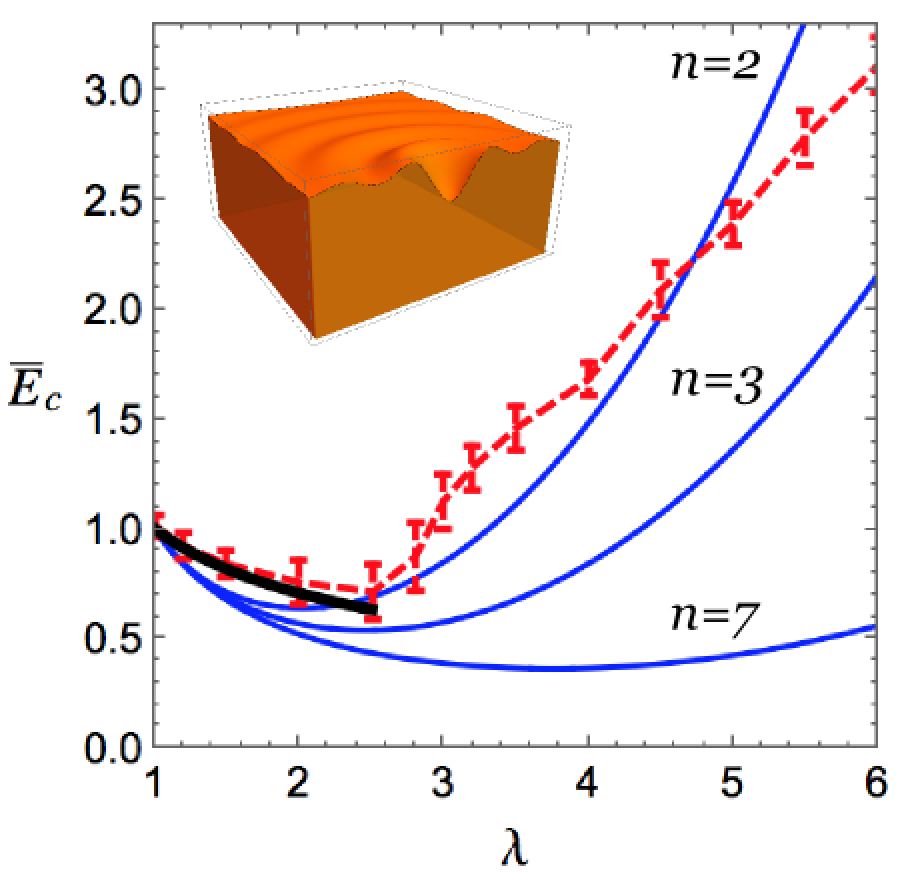
How much can a soft dielectric membrane stretch under a large voltage before it breaks? Soft dielectric membranes expand when put under a large voltage. That makes them prime candidates for futuristic soft devices such as artificial muscles and soft robots. Conversely, when they are deformed they produce an electric current and can thus in principle be used a energy harvesters. However, as they expand in two dimensions, they also thin out in the third, until the distance between the two faces is so small that an electrical breakdown occurs. In a paper published in Physical Review Letters, we derived a simple formula to predict the onset of this catastrophic thinning. |
|
|
 |
COMPUTATIONAL SOLID MECHANICS
|
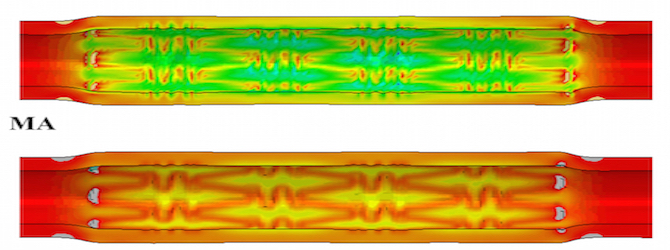
How can a computer simulate the behaviour of soft solids? Being able to describe and predict the behaviour of soft matter when it is deformed is a huge challenge of Applied Mathematics. The theory of Continuum Mechanics provides a physically sound framework for this enterprise, where the relevant mathematical equations can be derived rigorously from first principles. The main problem is that in general they are formidable non-linear coupled partial differential equations, for which there exist explicit solutions only in very special cases. For all other cases, we must turn to computer power to make progress. Finite Element Analysis is a computational method which has successfully solved countless, otherwise intractable, problems for deformed solids. It works perfectly fine for linear elasticity, where quantities are infinitesimally small. However, its extension to non-linear elasticity, where deformations can be as large as desired, has proved very difficult. In a series of papers we have explored the performance of existing commercial and open codes relying on FEA and unearthed some crucial problems, which must addressed before simulations can be expected to have a predictive power. |
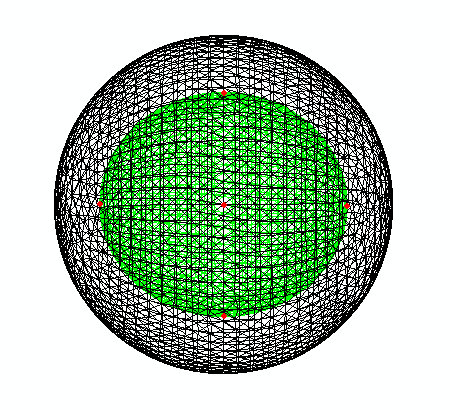
|
|
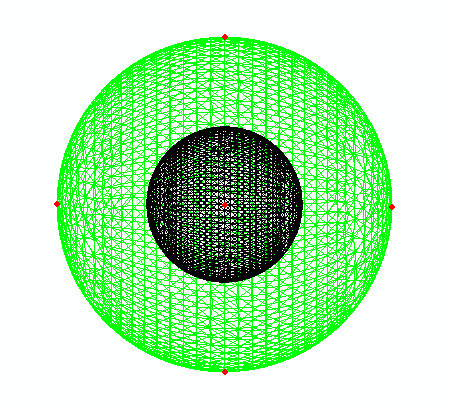 |
MECHANICS OF BRAIN MATTER
|
How does the brain deform during an impact? The geometrical properties of the brain are now almost perfectly established, with ever improving imaging techniques (Computational Tomography scans, Magnetic Resonance Imaging, etc.), which paint an amazingly accurate picture at microscopic level. On the other hand, very little is actually known about the physical properties of brain tissue. However, there are some crucial areas of research where the mechanical properties of the brain must be established with some degree of accuracy, such as in the numerical simulation of growth, swelling, surgery and injury scenarios, because brain matter then experiences deformations. For instance, the most severe type of brain trauma coincides with the appearance of Diffuse Axonal Injury, which can occur at stretches of about 30%, at strain rates of 10-120/s. Being able to propose a sound and tested model for brain matter behaviour at these levels represents a major challenge for Applied Mathematics, Mechanical Engineering and Biomedical Science, with far-reaching impact in biotechnology and huge potential benefits to society at large. We conducted a series of experiments on porcine brain matter, with a view to determine its mechanical properties at quasi-static to impact speeds. We used tensile, compressive and shear tests and found found that the latter protocol was best suited to brain matter which is tacky and brittle and does not lend itself well to the former two protocols. We then derived nonlinear models to describe and hopefully predict the behaviour of brain matter in impact and blast situations.Of course these tests were highly destructive; the next step is to come up with protocols for non-destructive evaluation of brain matter in vivo. |
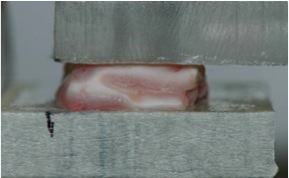
|
|
 |
MECHANICS OF SOFT TISSUES
|
Have you ever pinched or sheared a piece of meat? or your skin? Notice how wrinkles appear on the surface. However, when you deform a block of rubber or silicone, its surface stays smooth for much larger deformations. Why is that? In the search for explanations, one must look at the differences between elastomers (rubber, silicone, gels, etc.) and soft tissues (muscle, arteries, skin, etc.) and see if a difference in mechanical constitution leads to a significant difference in mechanical behaviour. For example, a striking difference is that elastomers are essentially isotropic (mechanical properties are the same in every direction) whilst soft tissues display anisotropic response, due to the presence of families of aligned collagen fibers (clearly visible to the naked eye on the picture). Another difference is that soft tissues under tension stiffen earlier than elastomers (typically, you can extend skin or arteries by 10 to 20 percent, but you can stretch a rubber band up to 8 to 10 times its original length, before severe stiffening occurs.) We are investigating how these different characteristics affect the mechanical behaviour of one type of material versus the other, with respect to stability studies and ultrasonic wave propagation. |
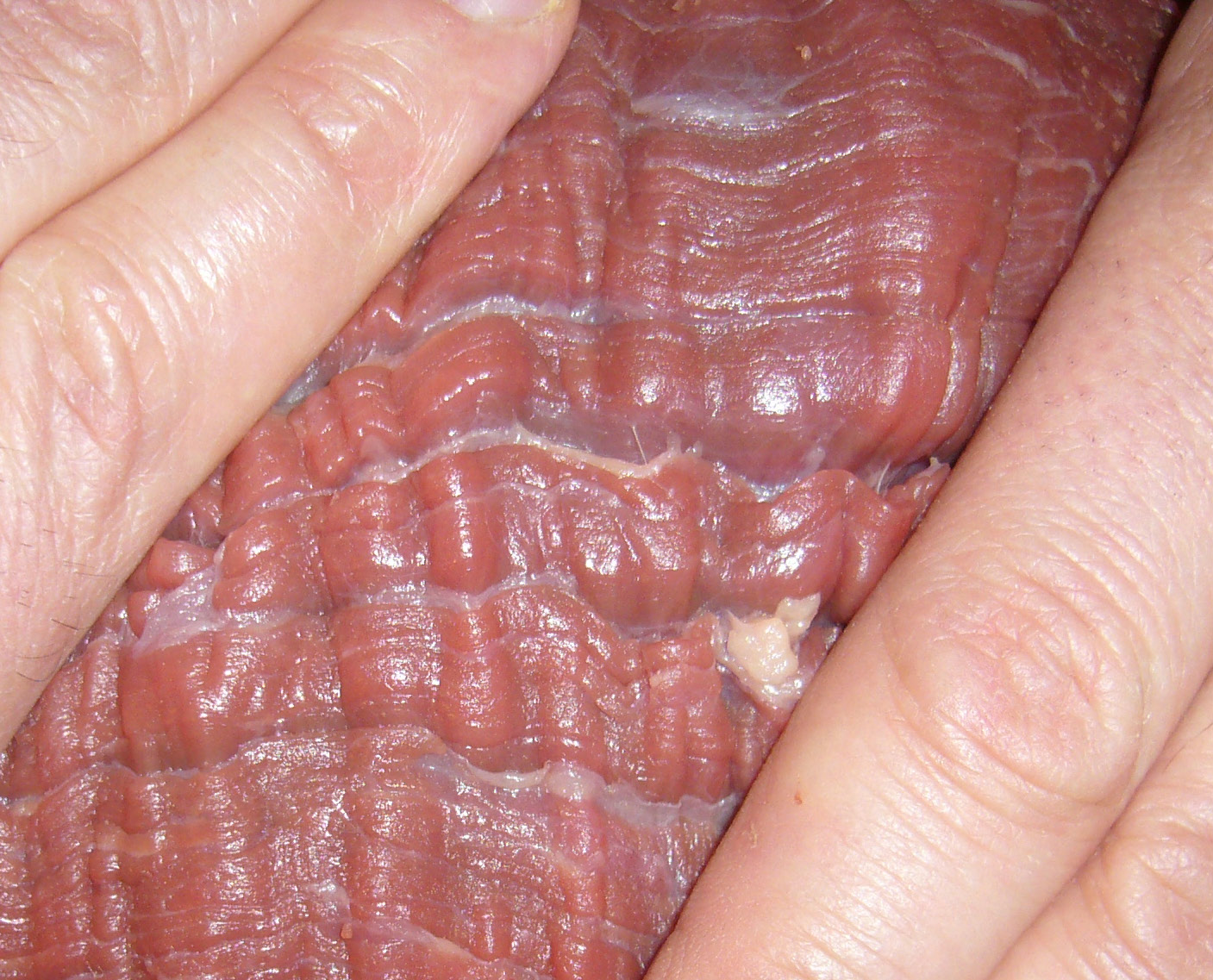
|
|
MECHANICS OF STABBING
|
How much force does it take to pierce the skin? Forensic experts are often asked that question in trials related to stabbing incidents. So far they can only invoke vague terms such as "mild", "moderate", "severe", etc. We investigated whether it is possible to quantify more accurately stabbing forces. For this project we received funding from the Irish Research Council (PhD funding), the Irish Department for Justice, Equality, and Law Reform (PhD funding), the National University of Ireland (Pierce Malone Scholarship), and the Royal Irish Academy (Ulysses grant), and the Region Ile-de-France (funding for Joint Dublin-Paris PhD).
|

|
.
|
 |
MECHANICS OF CORK-PULLING
|
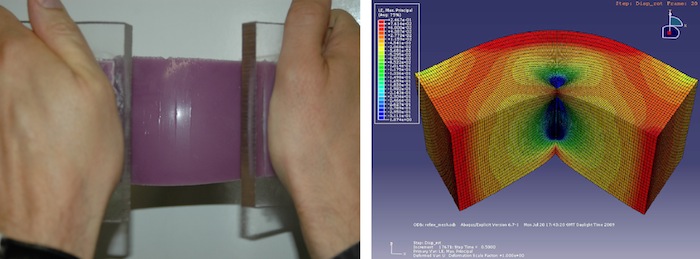
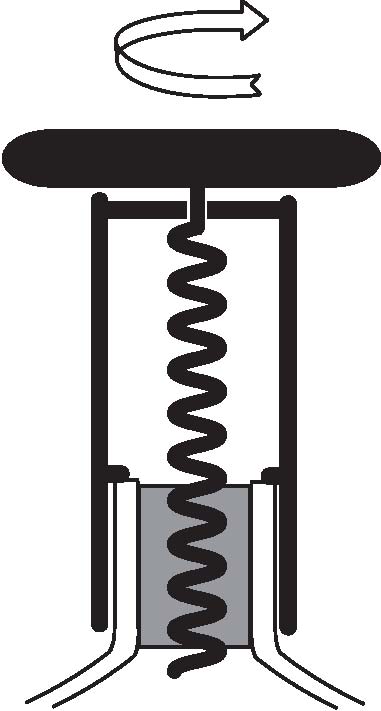
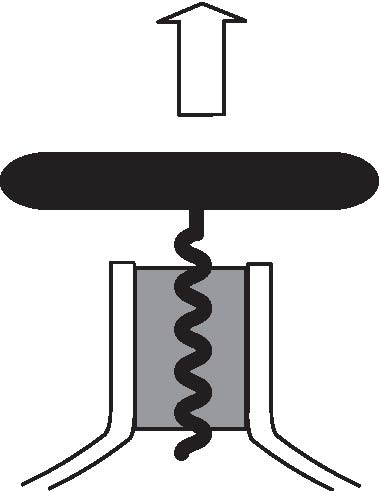
What kind of corkscrew system requires the least effort to uncork a bottle? In an article which appeared in the November 2007 issue of the Proceedings of the Royal Society A, we claimed that the theory of nonlinear elasticity could answer that classic wine party discussion. We provided a mathematical argument to those wine amateurs who favour a system relying on a combination of pulling and twisting (first picture on the right) over a system relying on pulling only (second picture on the right). Needless to say, this has been known for a long time by corkscrew manufacturers, who often promote the latter kind of corkscrew as "easy" or "magic".Of course, we were using this analogy as a gimmick, and wanted to give a "twist" to an otherwise quite mathematical argument. Our more serious point was that research in nonlinear elasticity should not leave aside the possibility of secondary fields in the so-called "semi-inverse method", because they are the rule rather than the exception (secondary deformation fields in nonlinear elasticity are the analogue of secondary flows in non-Newtonian fluids.) |
|
||||||||||||||
|
 |